Entangled Quantum-like Tokenomics for DeSci & Prediction Markets

Author: `sshmatrix` | `Antitoken` | quant/acc

Ping: `dev@antitoken.pro`

Terms $X, $Y and 'Catalyst' used in previous drafts have been replaced with $BARYON, $PHOTON and 'Collider' respectively.

This is a living document and will be updated in real time to match the development of the actual product.

Mission

$ANTI and $PRO are an experimental entangled token pair designed to explore new frontiers in decentralised market-making by introducing a system capable of encoding both predictable and unpredictable outcomes into its tokenomics. This approach challenges traditional continuous AMMs by employing a discretised mechanism where market dynamics are shaped by the interaction between the two tokens. Beyond their memetic origins, $ANTI and $PRO have potential use cases in decentralised science (DeSci), where such a system could underpin prediction markets for scientific research. By embedding structured uncertainty and dynamic equilibria into their design, these tokens offer a novel framework for creating markets that balance stability with probabilistic behavior, enabling a more nuanced approach to decentralised economies.

Technology

The $ANTI-$PRO token pair emerged as a bold experiment in tokenomics, exploring the potential of a system based on entangled market dynamics. Unlike traditional decentralised market-making, which relies on continuous automated market makers (AMMs) in individual pools, $ANTI and $PRO introduced a discretised AMM model where market-making occurs through paired interaction. Launched with an initial issuance of 0.1 SOL split asymmetrically between $ANTI (0.045 SOL) and $PRO (0.055 SOL), this system was designed to inherit a natural Delta (Δ), creating a dynamic from the outset. This asymmetry, combined with the social entanglement of the pair, led to emergent behaviors like parity maintenance and rewards optimised for holding both tokens. Rather than rely solely on theoretical modeling, the project embraced the memetic nature of cryptocurrency markets to test its viability in real-time. To expand the experiment, a custom AMM-like mechanism called the Collider contract will be introduced to bind $ANTI and $PRO, which mints two new tokens: Emission ($BARYON) and Radiation ($PHOTON). Governed by tunable functions F() and G(), these tokens encapsulate different dynamics: Emission is predictable and derived from the sum (N_ANTI + N_PRO), while Radiation is probabilistic and reacts to the difference (N_ANTI - N_PRO). This combination of deterministic and indeterministic outputs creates an environment of unique market interactions, where equilibria may form dynamically. The introduction of fluidity and randomness in the Radiation token presents an opportunity to observe how markets respond to unpredictable, yet systematically integrated, behaviors. While $ANTI and $PRO began as a memetokenomics experiment, their underlying mechanisms hint at significant potential applications, particularly in decentralised science (DeSci). In DeSci, systems frequently encode dualities, such as consistent and inconsistent components in a hypothesis. The Collider system could model these through Emission and Radiation tokens, enabling prediction markets for scientific validation or exploration. Beyond DeSci, the $ANTI-$PRO ecosystem has potential applications in decentralised organisations, prediction markets, and decentralised financial platforms where opposing yet interconnected forces — such as support vs. dissent or risk vs. reward — can be encoded directly into token mechanics. This whitepaper delves into these use cases and outlines a roadmap for exploring the broader implications of $ANTI and $PRO in decentralised systems.

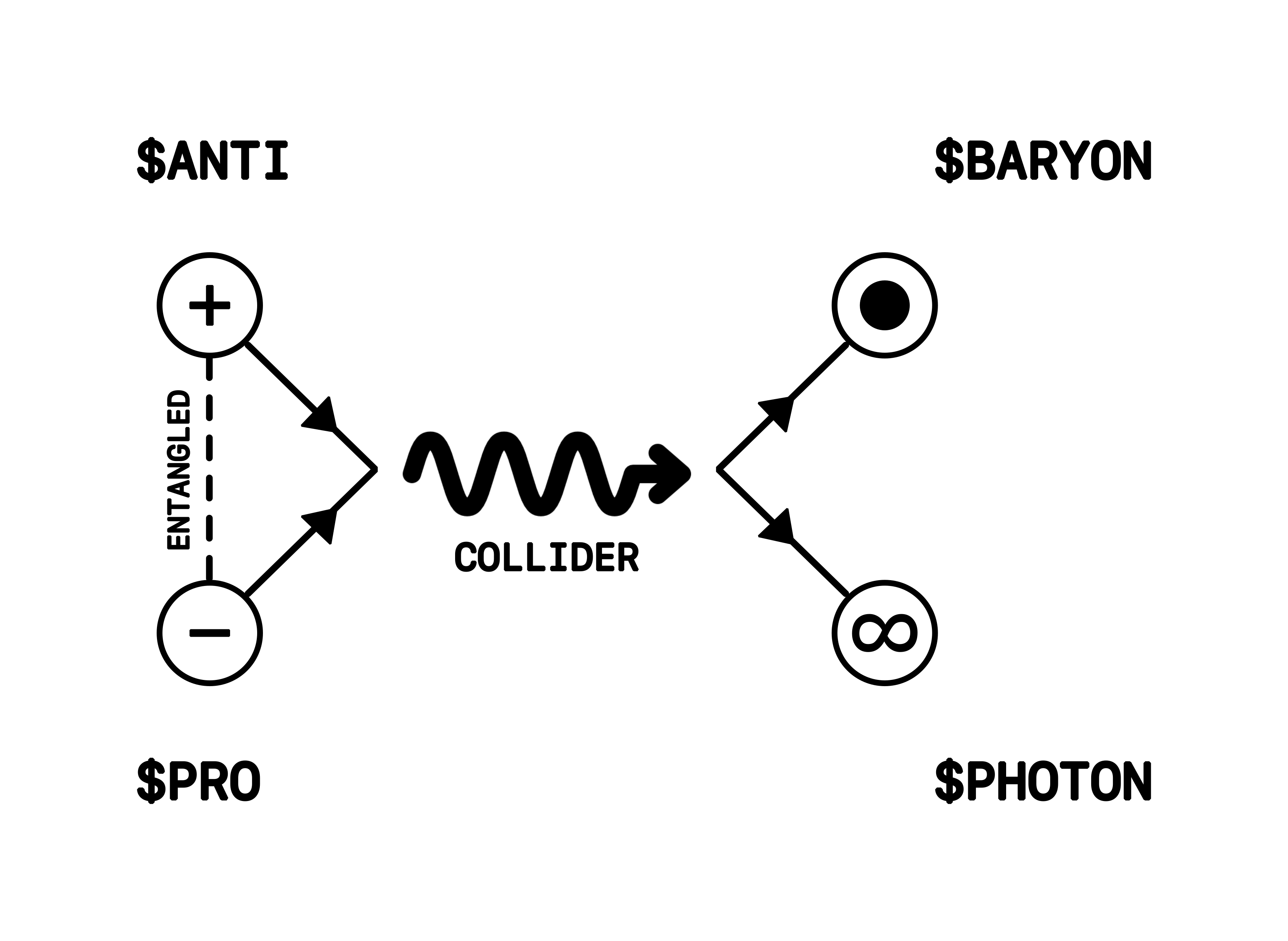
Figure 1: Concept

Quantum Binding

In analogy with fundamental principles in quantum mechanics, the behavior and interactions of $ANTI and $PRO tokens can be modeled using quantum wave functions, denoted as 𝜓^ANTI and 𝜓^PRO respectively. These wave functions represent the quantised states of the corresponding tokens. The Collider, serving as an operator in this quantum-inspired system, governs the transformation and emission of these tokens by acting on their wave functions.

The mathematical formalism of these transformations is given by the following forward relations:

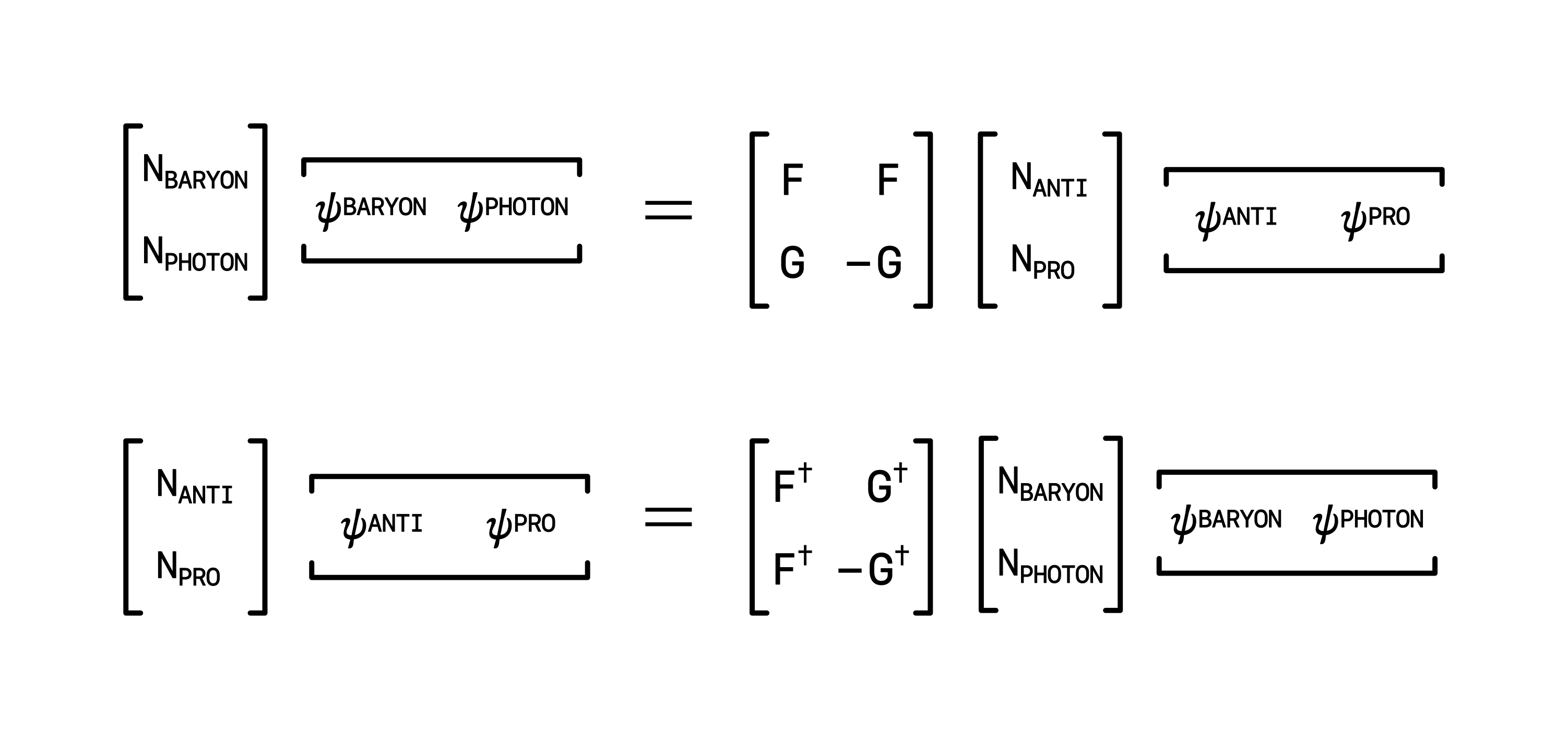
    N_X·𝜓^X = F(N_ANTI·𝜓^ANTI + N_PRO·𝜓^PRO), and

    N_Y·𝜓^Y = G(N_ANTI·𝜓^ANTI - N_PRO·𝜓^PRO), (1)

where N_X and N_Y represent the emitted quantities of $BARYON and $PHOTON tokens, respectively. The F(a) and G(b) denote tunable operations applied to their respective arguments a and b, which encapsulate the combined effects of the deposited wave functions N_ANTI·𝜓^ANTI and N_PRO·𝜓^PRO. These operations effectively serve as control mechanisms, enabling the Collider to regulate the transformation of deposited tokens into emitted tokens.

The inverse relations, which describe the process of depositing $BARYON and $PHOTON tokens to release $ANTI and $PRO tokens, are derived as:

    N_ANTI·𝜓^ANTI = F^†(N_X·𝜓^X)/2 + G^†(N_Y·𝜓^Y)/2, and

    N_PRO·𝜓^PRO = F^†(N_X·𝜓^X)/2 - G^†(N_Y·𝜓^Y)/2. (2)

Here, F^† and G^† are the respective inverse operations of F and G, providing a means to reverse the transformation and extract the original $ANTI and $PRO wave functions from the emitted tokens.

This duality of forward and inverse operations forms the basis for the Collider's functionality, enabling both the emission and recovery of tokens. The forward operation requires the deposition of $ANTI and $PRO tokens to emit $BARYON and $PHOTON tokens, while the inverse operation facilitates the reverse process, where depositing $BARYON and $PHOTON tokens results in the release of $ANTI and $PRO tokens. These operations are inherently interconnected and symmetrically defined by the functions F, G, F^† and G^†. The interplay of these operations is best visualised through a Feynman diagram-like schema, as illustrated in Figure 1. In this representation, the Collider is depicted as an interaction vertex where incoming wave functions (tokens) are transformed into outgoing wave functions, encapsulating the quantum-inspired dynamics and control mechanisms governing the token ecosystem.

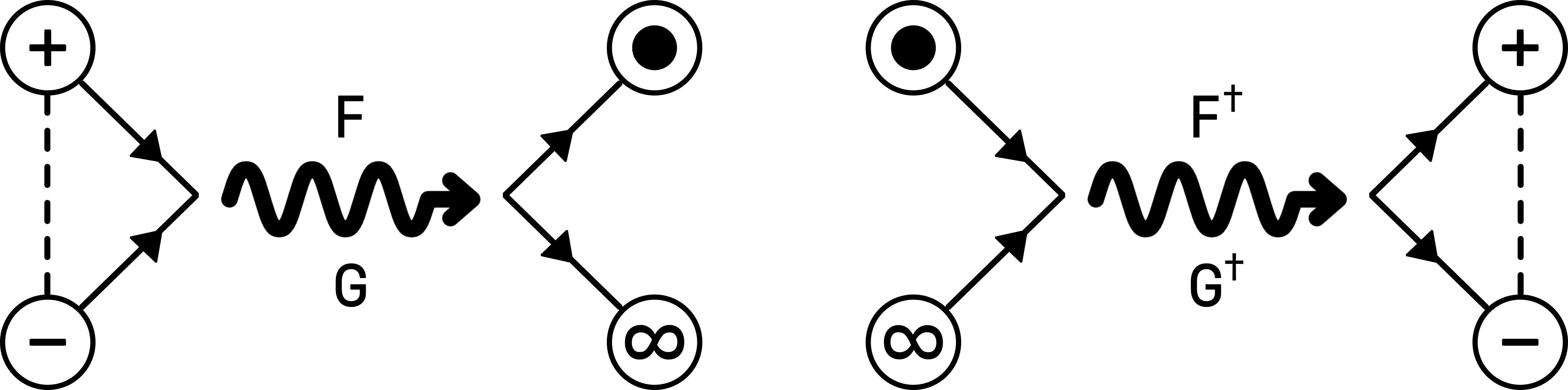
Figure 2: Forward and Inverse Operations

Forward and inverse operations (1) and (2) can be written in matrix form as follows:

An Example

Let’s work through an example of Alice and Bob interacting with the Collider. Suppose Alice and Bob deposit 15 $ANTI tokens and 10 $PRO tokens into the Collider. The forward operation in the Collider is described by:

    N_X·𝜓^X = F(N_ANTI·𝜓^ANTI + N_PRO·𝜓^PRO),

    N_Y·𝜓^Y = G(N_ANTI·𝜓^ANTI - N_PRO·𝜓^PRO).

Here, N_ANTI = 15 and N_PRO = 10, and F() and G() are operations that control how the deposited tokens transform into N_X·𝜓^X and N_Y·𝜓^Y. In the next step, the deposits are combined:

    N_ANTI·𝜓^ANTI + N_PRO·𝜓^PRO = 15 𝜓^ANTI + 10 𝜓^PRO,

    N_ANTI·𝜓^ANTI - N_PRO·𝜓^PRO = 15 𝜓^ANTI - 10 𝜓^PRO.

The Collider processes these using F() and G():

    N_X·𝜓^X = F(15 𝜓^ANTI + 10 𝜓^PRO),

    N_Y·𝜓^Y = G(15 𝜓^ANTI - 10 𝜓^PRO).

After processing, the outputs are calculated as N_X = 12 and N_Y = 4, indicating that Alice and Bob receive 12 $BARYON tokens and 4 $PHOTON tokens after processing by the Collider's operations.

If Alice and Bob decide to reverse the process to recover their original tokens, they deposit the 12 $BARYON tokens and 4 $PHOTON tokens back into the Collider. The inverse operations, defined by F^† and G^†, allow the Collider to determine the original deposits. By substituting and simplifying, the calculations confirm that the deposited 12 $BARYON tokens and 4 $PHOTON tokens yield 15 $ANTI tokens and 10 $PRO tokens, successfully restoring the initial amounts deposited by Alice and Bob.

    N_ANTI·𝜓^ANTI = F^†(12 𝜓^X)/2 + G^†(4 𝜓^Y)/2,

    N_PRO·𝜓^PRO = F^†(12 𝜓^X)/2 - G^†(4 𝜓^Y)/2.

The true forms of F, G, F^† and G^† are not provided in this paper, and they will only be revealed in the Collider contract upon deployment.

Properties of Collider

The Collider contract contains F, G, F^† and G^†, and these operators vary with each use-case, since each use-case has a unique inherent economy. There are in fact several possible choices of F, G, F^† and G^† in the Collider. However, construction of the Collider must follow a conservation principle:

• Completeness: Forward and inverse operations must be complete, i.e. users must not lose or make any excess tokens by performing a forward and inverse operation consecutively.

This part will be expanded once the Collider's exact form in revealed.

Note that each Collider is a unique contract and each set of emitted $BARYON and $PHOTON tokens are unique; a notation of $BARYON_k and $PHOTON_k is more appropriate.

Domain-specific Use-cases

Prediction Markets

Prediction markets are among the simplest applications of entangled tokenomics. The inherent duality in all decision-making is encoded in the core topology of $ANTI and $PRO tokenomics. This explicit duality not only enables more precise and pointed predictions but also allows for quantifiable measures of uncertainty.

In this example, we explore how Bob uses the Collider to express his prediction of an event's likelihood and how his holdings are affected when the actual outcome differs. Bob believes there is a 70-30 chance that a particular event will occur, representing his confidence in the event happening versus not happening. To express this belief, Bob deposits 70 $PRO tokens and 30 $ANTI tokens into the Collider. The Collider processes these inputs through its forward operations, which reflect Bob's prediction and uncertainty. The forward transformation combines the deposited tokens, applies the operations F and G, and produces outputs defined by these functions, resulting in the emission of 33 $BARYON tokens and 24 $PHOTON tokens. The significance of these token emissions and the subsequent impact of the actual outcome on Bob's holdings provide a quantitative demonstration of the Collider's functionality.

Bob interacts with the Collider by depositing 70 $PRO tokens and 30 $ANTI tokens, reflecting his belief in a 70-30 probability of an event occurring. The Collider processes these inputs using its forward operations, resulting in the emission of 33 $BARYON tokens and 24 $PHOTON tokens. The forward transformation combines the deposited tokens, applies the operations F and G, and produces outputs defined by these functions.

If the final outcome differs from Bob's prediction and the event's inverse occurs with a 60-40 margin, Bob experiences a loss. Specifically, he loses 25 $BARYON tokens and 8 $PHOTON tokens. Bob's loss in $BARYON tokens is significant because he incorrectly predicted the direction of the outcome. However, his loss in $PHOTON tokens is relatively minor, as his prediction of uncertainty was closer to the actual result.

To reverse the process, Bob can deposit the remaining 8 $BARYON tokens and 16 $PHOTON tokens into the Collider. The inverse operations, defined by F^† and G^†, calculate the corresponding amounts of original tokens. Upon completing the inverse transformation, Bob recovers 35 $PRO tokens and 17 $ANTI tokens, successfully closing the loop and reflecting the updated outcome in his token holdings.

In the above example, the functions F, G, F^†, and G^† were assumed to be independent of any external influences or biases resulting from the question itself. This ensures that the transformations performed by the Collider are purely based on the tokens deposited and the inherent mathematical properties of the operations, rather than being influenced by the context or framing of the question. Such independence highlights the neutrality of the Collider's mechanism, allowing the outcomes to be determined solely by the quantitative inputs and the predefined rules of the system.

THE EQUALISER

The Equaliser is a separate contract designed to handle the redistribution of tokens in scenarios where such redistribution is a desired feature. One prominent use case is prediction markets, where redistribution is needed as a function of the prediction's proximity to the final truth. In other use cases, such functionality may not be necessary; for example, in DeSci, redistribution may not be relevant.

In the earlier example, the loss sustained by Bob due to his incorrect prediction is determined by the Equaliser. The Equaliser operates in a manner analogous to the concept of superposition in quantum physics. The emitted $BARYON and $PHOTON tokens are tunnelled into the Equaliser, which then determines the extent of win or loss (Λ) by taking the inner product ⟨·,·⟩ of the predicted probability distribution φ - determined by the deposited $ANTI and $PRO, and the actual truth distribution χ, such that

Λ = ⟨φ,χ⟩/⟨χ,χ⟩. (3)

Since the inner products are contiguous over their domain, the tokens in the Equaliser's pool can be redistributed among the participants through a straightforward mapping mechanism. This ensures that token redistribution is proportional to the accuracy of individual predictions while accounting for the collective contribution of all participants.

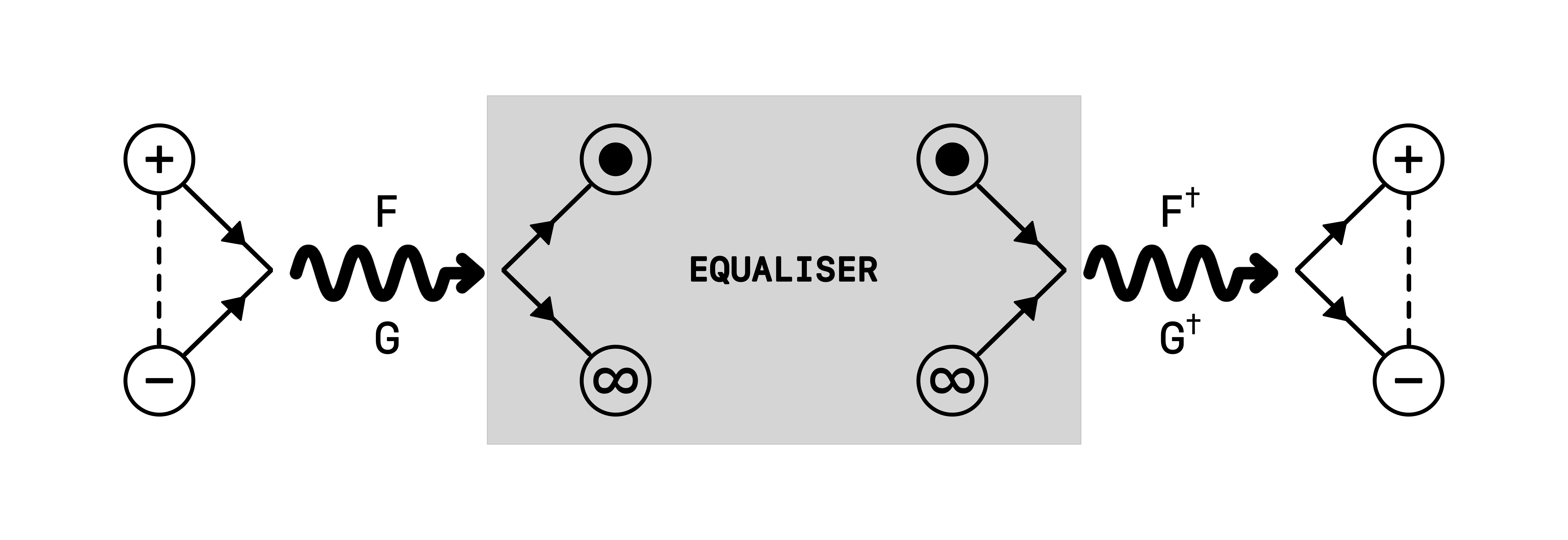
Figure 3: Prediction Markets

Decentralised Science

DeSci (Decentralised Science) is another domain where $ANTI and $PRO tokens can be utilised in various settings. These tokens can be employed to programmatically fund DeSci projects, where project outcomes are encoded from their raw form into a numerical range through appropriate mapping. Alternatively, emitted tokens can serve as a market for citizen science resources, such as distributed computing. Below are two illustrative examples:

Funding Scientific Trust

Consider a scenario where Alice is interested in funding a DeSci project that aims to determine the efficacy of a pharmaceutical product, "Drug X." Alice funds the research by depositing $ANTI and $PRO tokens in a proportion she deems appropriate, based on her assessment of the project's likelihood of success. In this case, the Equaliser contract is unnecessary since no outcome-based redistribution in intended; however, alternative methods must exist to ensure the emitted tokens are effectively utilised. The $BARYON tokens (representing Alice's trust in the outcome) are directly used to fund the project on which Alice has voted, while the $PHOTON tokens (representing her uncertainty about the outcome) are released into her personal wallet. Alice can then choose to expose the $PHOTON tokens to the market via selling, lending, staking etc or retain them. If the project succeeds, the market value of both $BARYON and $PHOTON tokens is likely to increase. Alice can then decide whether to sell her $PHOTON tokens for profit or acquire additional $BARYON tokens from the market to tunnel the dual pair back into $ANTI and $PRO tokens. Note that it is also possible for the token prices to decrease upon success due to external influences, such as the internal proceedings - including but not limited to the tokenomics - of the DeSci project in question. The market-making model in this case must be carefully designed to prevent any leakage of monetary value during token dispersion after emission, irrespective of the direction or magnitude of the price movement of the token pair.

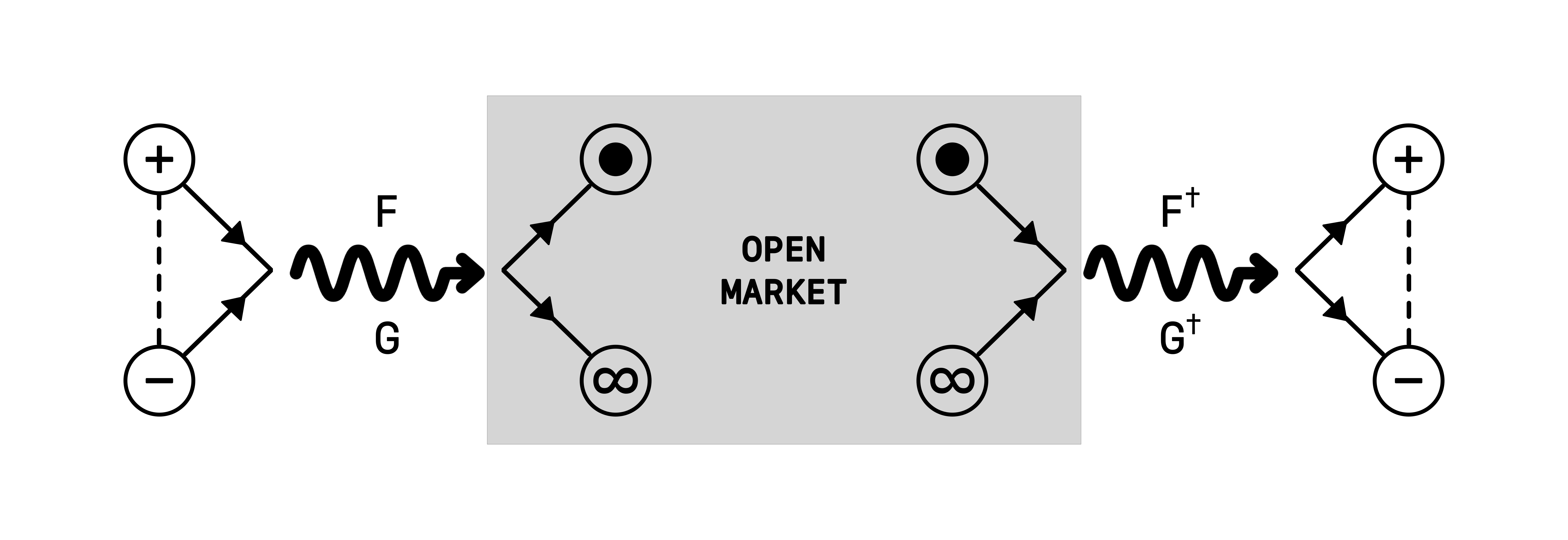
Figure 4: Funding Decentralised Science

Distributed Crowd-sourcing

The application of these tokens in distributed volunteer computing is both significant and intuitive. For instance, Bob has idle devices he wishes to rent out for projects requiring high-throughput parallel computing. Through programmes such as BOINC, Bob can lend his computing resources and earn $BARYON and $PHOTON tokens as rewards. Bob can subsequently tunnel these tokens back into $ANTI and $PRO, or sell them in the local market to others seeking computing resources. Alternatively, if Bob required computing resources himself, he would deposit $ANTI and $PRO tokens in appropriate proportions to emit $BARYON and $PHOTON tokens, which he could then use to purchase compute resources from the local market. In this example, the $BARYON_k and $PHOTON_k tokens are typically degenerate (although this is a flexible property and can be broken), holding equal value. This straightforward application demonstrates pronounced flexibility in how the tokens can alternate between markets and utilities.

Local market in this case refers to the $BARYON_k and $PHOTON_k pairs. 'Degenerate' refers to the state where $BARYON_k and $PHOTON_k have indistinguishable properties.

The applications of $ANTI and $PRO tokens in DeSci are vast, although their human interfaces are still under development to ensure completeness and usability. In both examples, it is worth noting that the local market for each use-case is determined by the emitted $BARYON and $PHOTON tokens, while the $ANTI and $PRO tokens remain within a global market independent of specific contexts or use-cases. Detailed technical specifications for the examples provided will be included in the forthcoming yellow paper.

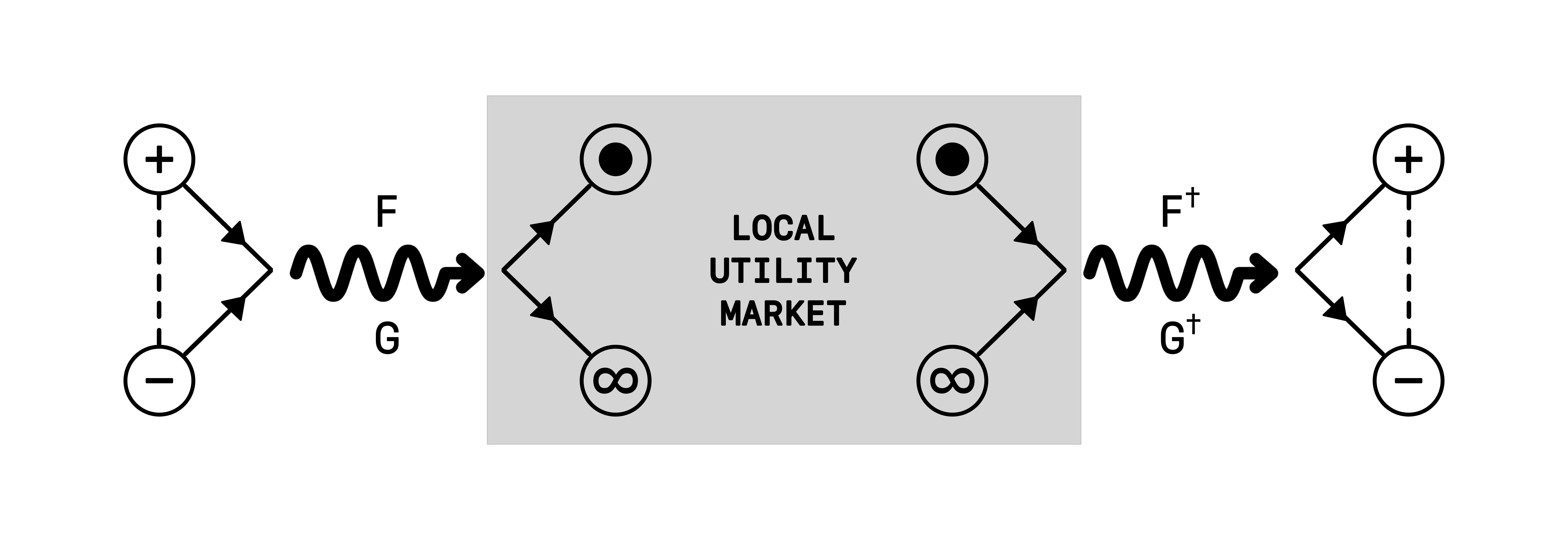
Figure 5: Science Resources Marketplace

Conclusion

In conclusion, the $ANTI-$PRO token ecosystem presents a pioneering approach to decentralised market-making, blending deterministic and probabilistic dynamics to address limitations in traditional automated market-making systems. By embedding dualities and leveraging entangled behaviours, the system enables nuanced applications across domains, from prediction markets to decentralised science (DeSci). The introduction of the Collider contract and its transformative operations adds layers of complexity and flexibility, allowing the creation of bespoke markets with features tailored to specific needs.

The use of $BARYON and $PHOTON tokens to encode trust and uncertainty, respectively, highlights the system's adaptability. In DeSci, this translates into streamlined funding models and resource distribution mechanisms, while in prediction markets, the Equaliser ensures proportional reward redistribution based on accuracy. The architecture also mirrors quantum mechanical principles, ensuring completeness and reversibility in token transformations — a key innovation that preserves systemic integrity.

As this experimental tokenomics model matures, its potential applications could extend to other decentralised financial systems, governance frameworks, and resource-sharing networks, fostering innovation in markets that demand both stability and adaptability. While still in development, the system’s human interfaces and technical specifics promise to make this groundbreaking framework more accessible and applicable across a wide array of use cases.

Figure 6: The Antitoken Collective

Further details on implementation, along with a deeper exploration of the mathematical foundations, will be presented in the upcoming yellow paper, paving the way for new standards in decentralised economic systems.